Шалгалт
Бодлогын хариу нь ширхэг бодлогоос ширхгийг сонгох боломжийн тоотой тэнцүү.
Бодолт 1
#include <iostream>
using namespace std;
int f[20], i, n, k;
int main() {
cin >> n >> k;
f[0] = 1;
for (i = 1; i <= n; i ++)
f[i] = f[i-1] * i;
cout << f[n] / (f[n-k] * f[k]);
return 0;
}
Бодолт 2
ширхэг бодлогоос ширхэгийг сонгох боломжийн тоо нь дараах хоёрын нийлбэртэй тэнцүү.
- Сонгосон дотор дүгээр бодлого орсон байх боломжийн тоо нь -тэй тэнцүү.
- Сонгосон дотор дүгээр бодлого ороогүй байх боломжийн тоо нь -тай тэнцүү.
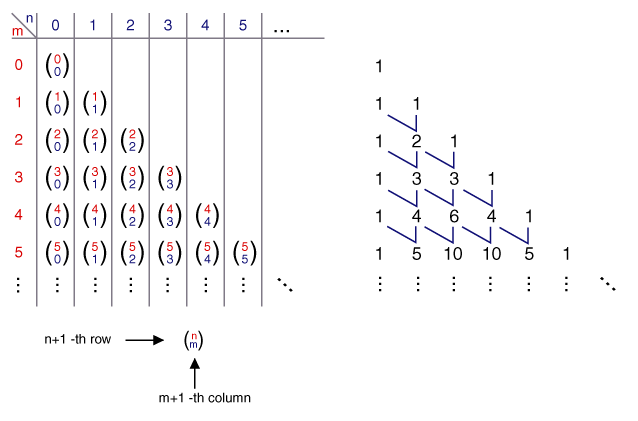
Паскалын гурвалжинтай адил юм.
#include <iostream>
using namespace std;
int main(){
int a, b, c[30][30], i, j;
cin >> a >> b;
for (i = 0; i <= 10; i++){
c[i][0] = 1;
c[i][1] = i;
for (j = 2; j <= i; j++)
c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
}
cout << c[a][b] << endl;
return 0;
}